Introducción al clustering (I): algoritmo k-means
¿Qué es el aprendizaje no supervisado?
En el machine learning, las técnicas de aprendizaje no supervisado nos permiten descubrir estructuras ocultas en los datos. A diferencia del aprendizaje supervisado, en este caso no trabajamos con datos etiquetados para entrenar los modelos, ya que el objetivo no es predecir la clase de salida.
De esta manera, al no contar con datos etiquetados, sólo podemos descubrir los patrones que se producen de forma natural en el conjunto de datos.
Una de las principales técnicas del aprendizaje no supervisado es el clustering. El objetivo del clustering consiste en encontrar grupos de instancias (llamados clusters) que están relacionadas entre sí.
Esta técnica tiene innumerables aplicaciones como la detección de outliers, la segmentación de clientes o los sistemas de recomendación.
Hay diferentes tipos de algoritmos de clustering y cada uno de ellos elige los clusters de manera distinta. En este artículo nos centraremos en el popular algoritmo k-means, el cual busca instancias centradas en un punto determinado, llamado centroide. Después de explicar su funcionamiento, lo aplicaremos en Python a un conjunto de datos y visualizaremos los resultados obtenidos.
Funcionamiento del algoritmo k-means
El algoritmo k-means es un método de clustering muy utilizado que coge cada punto de nuestro dataset e intenta asignarle un grupo o clúster de manera iterativa. El objetivo es asignar cada punto a un grupo en base a la similitud de sus características.
De esta manera, los pasos que sigue el algoritmo k-means para encontrar los grupos en función de nuestros datos son los siguientes:
- Se eligen de manera aleatoria las coordenadas de los k centroides iniciales del conjunto de datos. Los centroides son los puntos que marcan el centro de cada agrupación
- Una vez se han inicializado los centroides, se agrupan cada punto con el centroide más cercano. Para ello se utiliza una medida de distancia como la distancia euclídea.
- Se actualizan los centroides cambiando su posición al centro de las muestras que le fueron asignadas.
- Se repiten los pasos 2 y 3 hasta que se cumpla un cierto criterio de parada establecido por el usuario. Estos criterios de parada pueden ser:
- Las asignaciones de clústeres no cambian o se alcanza un umbral de tolerancia definido.
- Se alcanza un número máximo de iteraciones.
Para saber que agrupamiento es mejor y poder recalcular los centroides iterativamente, deberemos utilizar una función que nos permita calcular la distancia entre dos puntos x e y. La función de distancia que normalmente se utiliza en clustering es la distancia euclídea al cuadrado:
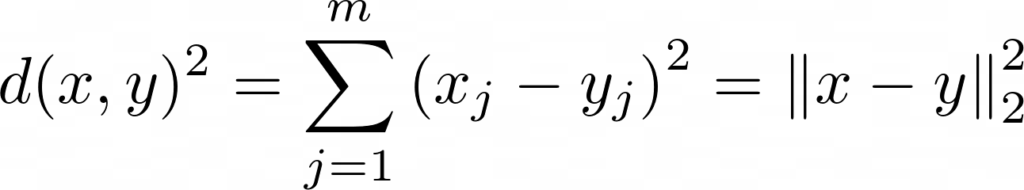
donde m es el número de dimensiones de nuestros datos.
Cuando se utiliza la distancia euclídea, la idea del algoritmo consiste en elegir los centroides que minimicen la suma de errores al cuadrado (SSE):
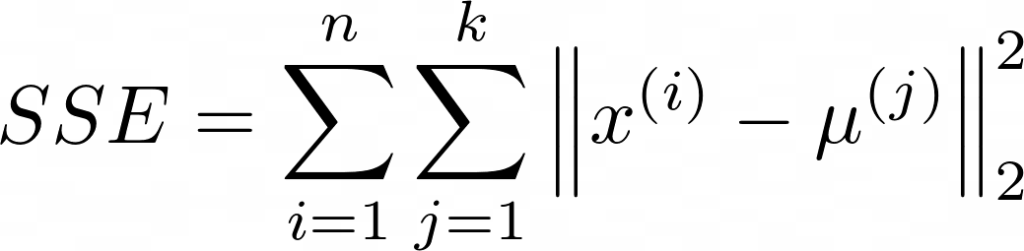
donde k es el número de grupos y μ(j) es el centroide del cluster j.
Veamos ahora como aplicarlo a nuestros datos!
Aplicando el k-means a nuestro conjunto de datos
Una vez hemos aprendido el funcionamiento de este algoritmo, veamos cómo aplicarlo a nuestro conjunto de datos. Aunque k-means puede aplicarse a datos de mayor dimensión, en este tutorial vamos a utilizar datos bidimensionales para poder visualizarlos de manera sencilla.
En primer lugar, cargamos en conjunto de datos y lo convertimos en un Dataframe de Pandas:
import pandas as pd
# Cargamos el conjunto de datos
df = pd.read_csv ('data/data.csv')
# Mostramos las primeras observaciones
df.head()
A continuación, mostramos una gráfica de dispersión con todos los puntos para buscar agrupaciones entre los datos:
import matplotlib.pyplot as plt
# Mostramos un diagrama de dispersión
df.plot.scatter(x='x', y='y', c='DarkGreen')
plt.show()
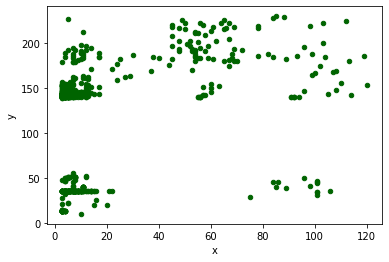
Como podemos ver en la anterior gráfica, hay 5 grupos bastante bien diferenciados, por lo que elegiremos 5 clústers.
Es recomendable estandarizar o normalizar los datos antes de aplicarles el algoritmo k-means en el caso de que no tengan la misma escala. En este caso utilizamos la clase MinMaxScaler de de scikit-learn que normaliza todos los datos entre unos límites definidos, por defecto entre 0 y 1.
from sklearn.preprocessing import MinMaxScaler
# Normalizamos los datos
min_max_scaler = MinMaxScaler()
df = min_max_scaler.fit_transform(df)
df = pd.DataFrame(df) # Convertimos a Dataframe
Veamos el resultado después de transformar las variables:
# Mostramos los datos escalados
df.head(5)
KMeans de la librería scikit-learn pasándole como argumento los siguientes parámetros:
n_clusters: el número de clusters y de centroides a generar. En este caso utilizaremos 5.n_init: método de inicialización. Para este ejemplo utilizamos la opción “random”, que se encarga de elegir n_clusters observaciones (filas) al azar de los datos para los centroides iniciales.max_iter: número máximo de iteraciones del algoritmo k-means para una sola ejecución.random_statedetermina la generación de números aleatorios para la inicialización del centroide.
Por supuesto, hay más parámetros para tener en cuenta y que podéis consultar en la documentación de scikit-learn, pero en este tutorial solo utilizaremos los anteriores descritos.
En el siguiente código mostramos como aplicar k-means a nuestro dataset:
from sklearn.cluster import KMeans
# Aplicamos k-means a nuestro dataset
km = KMeans(n_clusters=5, init='random',
max_iter=200, random_state=0)
y_km = km.fit_predict(df)
Así de fácil. Ahora veamos como podemos visualizar los resultados obtenidos.
Visualizando los grupos
Una vez ya tenemos el cluster asignado a cada observación, vamos a visualizarlos junto con la localización de los centroides. Para ello, utilizamos el siguiente código:
# Gráfico con los puntos y su cluster y los centroides
plt.figure(figsize=(8,8))
plt.scatter(df[y_km == 0][0], df[y_km == 0][1],
s=50, c='green', marker='o',
edgecolor='black', label='cluster 1')
plt.scatter(df[y_km == 1][0], df[y_km == 1][1],
s=50, c='orange', marker='s',
edgecolor='black', label='cluster 2')
plt.scatter(df[y_km == 2][0], df[y_km == 2][1],
s=50, c='lightblue', marker='v',
edgecolor='black', label='cluster 3')
plt.scatter(df[y_km == 3][0], df[y_km == 3][1],
s=50, c='purple', marker='d',
edgecolor='black', label='cluster 4')
plt.scatter(df[y_km == 4][0], df[y_km == 4][1],
s=50, c='brown', marker='p',
edgecolor='black', label='cluster 5')
plt.scatter(km.cluster_centers_[:, 0],
km.cluster_centers_[:, 1], s=200,
marker='*', c='red',
edgecolor='black', label='centroides')
plt.legend(loc="best")
plt.grid()
plt.show()
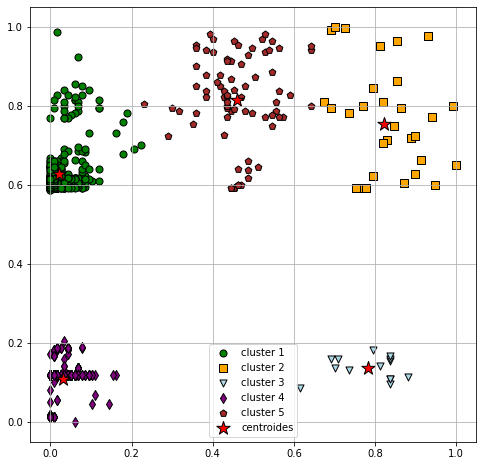
En el gráfico anterior podemos ver los puntos coloreados según el cluster al que pertenecen.
Como hemos visto, en este algoritmo de clustering es necesario especificar el número de clusters que queremos a priorio. Este es el mayor inconveniente de este método, ya que si elegimos un número de clusters inadecuado puede afectar negativamente a su rendimiento
Hay varios métodos para elegir el número óptimo de clústers a utilizar en el algoritmo. Una de las técnicas que se utiliza comúnmente es la gráfica elbow.
En este tutorial, hemos explicado el funcionamiento del algoritmo de clustering k-means y como se aplica a un conjunto de datos en Python. En futuras publicaciones mostraremos como obtener el número óptimo de clusters y otros métodos de agrupamiento, como, por ejemplo, el jerárquico.
Por último, recordar que todo el código utilizado en este tutorial se puede descargar desde nuestro repositorio de Github.




















