Pruebas de Hipótesis: Teoría y ejemplos prácticos
La estadística es una herramienta poderosa que nos permite tomar decisiones informadas basadas en datos. Uno de los conceptos fundamentales en estadística es el de las pruebas de hipótesis. Las pruebas de hipótesis son un procedimiento estadístico que se utiliza para evaluar afirmaciones o suposiciones sobre una población en función de una muestra de datos. En este artículo, exploraremos en profundidad las pruebas de hipótesis, su importancia en la investigación y la toma de decisiones, y proporcionaremos un ejemplo detallado para ayudar a comprender cómo funcionan.
¿Qué son las pruebas de hipótesis?
Las pruebas de hipótesis son un enfoque sistemático para evaluar afirmaciones o suposiciones sobre una población. En esencia, implican comparar dos hipótesis: la hipótesis nula (H0) y la hipótesis alternativa (H1). La hipótesis nula es una afirmación que generalmente refleja la «situación estándar» o la falta de un efecto. La hipótesis alternativa, por otro lado, es la afirmación que estamos tratando de probar.
En una prueba de hipótesis, el objetivo es determinar si los datos recopilados de una muestra son suficientemente diferentes de lo que se esperaría bajo la hipótesis nula. Esto implica calcular una estadística de prueba y determinar su probabilidad de ocurrencia bajo la hipótesis nula.
Ejemplo de pruebas de hipótesis
Supongamos que trabajas en una fábrica de galletas y eres responsable de asegurarte de que las galletas se produzcan con un peso promedio de 20 gramos. Sin embargo, has notado que algunas galletas parecen más pesadas de lo que deberían. Para investigar este problema, decides llevar a cabo una prueba de hipótesis.
Paso 1: Formulación de Hipótesis
- Hipótesis Nula (H0): La media de peso de las galletas es igual a 20 gramos (μ = 20 gramos).
- Hipótesis Alternativa (H1): La media de peso de las galletas es diferente de 20 gramos (μ ≠ 20 gramos).
En este caso, H0 refleja la situación estándar en la que las galletas tienen un peso promedio de 20 gramos, mientras que H1 sugiere que el peso promedio de las galletas es distinto de 20 gramos.
Paso 2: Recopilación de datos
Reúnes una muestra aleatoria de 30 galletas y registras sus pesos. Luego, calculas la media muestral, que resulta ser de 20.5 gramos, y la desviación estándar muestral, que es de 1.2 gramos.
Paso 3: Elección de un nivel de significación
El nivel de significación (alfa, α) es la probabilidad de cometer un error de Tipo I, que implica rechazar incorrectamente la hipótesis nula cuando es verdadera. Un valor común para α es 0.05, lo que significa que estamos dispuestos a aceptar un 5% de probabilidad de cometer un error de Tipo I.
Paso 4: Cálculo de la estadística de prueba
Para calcular la estadística de prueba, utilizamos la fórmula de la prueba t de Student:
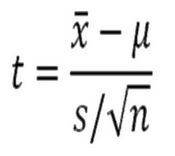
Donde:
- t es el valor de la Distribución t.
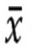es la media de la muestra (20.5 gramos).- μ es la media poblacional (20 gramos).
- es la desviación estándar de la muestra (1.2 gramos).
- n es el tamaño de la muestra (30 galletas).
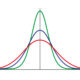
Aquí podéis encontrar un artículo donde explicamos en detalle esta distribución y su funcionamiento.
Sustituyendo los valores en la fórmula, obtenemos que t = 2.13.
Paso 5: Cálculo del Valor Crítico y P-Valor
El valor crítico es el punto de corte que separa la región de rechazo de la región de no rechazo. En este caso, como estamos realizando una prueba bilateral (μ ≠ 20 gramos), necesitamos buscar los valores críticos en la tabla de la distribución t de Student para un nivel de significación de 0.05 y 29 grados de libertad (30-1). Encontramos que tα/2 es aproximadamente ±2.045.
El p-valor es la probabilidad de observar una estadística de prueba al menos tan extrema como la calculada bajo la hipótesis nula. Para una prueba bilateral, calculamos el p-valor como el doble del área en la cola de la distribución:
p − valor = 2 × P(T > ∣t∣ )
Donde T es una variable aleatoria t con 29 grados de libertad. Utilizamos la calculadora estadística o software para encontrar el p-valor asociado a t=2.13, que resulta ser aproximadamente 0.041.
Paso 6: Toma de decisión
- Si ∣t∣ > tα/2: Rechazamos la hipótesis nula.
- Si ∣t∣ ≤ tα/2: No rechazamos la hipótesis nula.
En nuestro ejemplo, ∣2.13∣ > 2.045, por lo que rechazamos la hipótesis nula. Esto significa que hay evidencia suficiente para concluir que el peso promedio de las galletas es diferente de 20 gramos.
Paso 7: Conclusión
Basándonos en los resultados de la prueba de hipótesis, podemos concluir que las galletas no tienen un peso promedio de 20 gramos, lo que sugiere que podría haber un problema en el proceso de producción que necesita ser investigado y corregido.
Importancia de las pruebas de hipótesis
Las pruebas de hipótesis desempeñan un papel fundamental en la toma de decisiones basadas en datos en una variedad de campos, desde la industria hasta la investigación científica. Al seguir un enfoque estructurado y objetivo, las pruebas de hipótesis permiten a las personas tomar decisiones informadas y evitar conclusiones precipitadas o sesgadas.
En resumen, las pruebas de hipótesis son una herramienta esencial en el mundo de la estadística y la ciencia de datos. Ayudan a determinar si los resultados observados son consistentes con las afirmaciones hechas en una hipótesis nula o si se requiere una revisión de las suposiciones subyacentes. La aplicación adecuada de las pruebas de hipótesis puede marcar la diferencia en la toma de decisiones fundamentales en una amplia gama de contextos.
Al comprender y utilizar adecuadamente las pruebas de hipótesis, podemos tomar decisiones más fundamentadas y basadas en evidencia en una variedad de situaciones. Esperamos que este artículo haya arrojado luz sobre el concepto de pruebas de hipótesis y cómo se aplican en la práctica.
En el siguiente artículo, exploraremos ejemplos prácticos de pruebas de hipótesis en Python. Veremos cómo implementar estas pruebas utilizando el lenguaje de programación Python y bibliotecas estadísticas para realizar análisis de datos y tomar decisiones basadas en evidencia de manera efectiva. ¡No te lo pierdas!
