Aplicación de la Distribución t de Student en Python: Ejemplos prácticos
En nuestro artículo anterior, exploramos en detalle la Distribución t de Student, su historia, propiedades y aplicaciones en estadística. Hoy, llevaremos ese conocimiento al siguiente nivel al explorar cómo aplicar la Distribución t en Python para realizar pruebas de hipótesis y estimar intervalos de confianza. La Distribución t es una herramienta poderosa en el arsenal de cualquier analista de datos, y su implementación en Python facilita su uso en la práctica.
Antes de profundizar en su aplicación en Python, recordemos algunas de las características clave de la Distribución t de Student:
- La Distribución t es especialmente útil cuando trabajamos con muestras pequeñas y desconocemos la varianza poblacional.
- Se utiliza para realizar pruebas de hipótesis sobre la media de una población y para estimar intervalos de confianza.
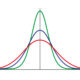
- La forma de la Distribución t se determina por el número de grados de libertad (df), que se calcula como n−1 para una muestra de tamaño n.
- Así, cuanto mayor sea el número de grados de libertad, más se asemejará la Distribución t a una Distribución normal.
Aplicación de la Distribución t de Student en Python
Python es una herramienta versátil para realizar análisis estadísticos, y la biblioteca scipy proporciona funciones para trabajar con la Distribución t. Veamos algunos ejemplos de su aplicación en Python.
Ejemplo 1: Prueba de Hipótesis con la Distribución t en Python
En este ejemplo, supongamos que tenemos una muestra de calificaciones de dos grupos de estudiantes (Grupo A y Grupo B) y queremos determinar si existe una diferencia significativa en sus promedios. Realizaremos una prueba de hipótesis utilizando la Distribución t en Python.
import scipy.stats as stats
# Datos de las calificaciones de los dos grupos
grupo_a = [85, 90, 92, 88, 87, 84, 91, 89, 86, 87]
grupo_b = [78, 82, 80, 88, 86, 79, 83, 81, 85, 84]
# Realizamos una prueba t de dos muestras independientes
t_stat, p_valor = stats.ttest_ind(grupo_a, grupo_b)
# Establecemos un nivel de significancia (alfa)
alfa = 0.05
# Comprobamos si rechazamos la hipótesis nula
if p_valor < alfa:
print("Hay una diferencia significativa entre los grupos.")
else:
print("No hay evidencia de una diferencia significativa entre los grupos.")
Este código utiliza la función ttest_ind de scipy.stats para realizar una prueba t de dos muestras independientes y determinar si existe una diferencia significativa entre los grupos A y B.
Ejemplo 2: Estimación de Intervalos de Confianza con la Distribución t en Python
Supongamos que deseamos estimar un intervalo de confianza del 95% para la media de una muestra de calificaciones. Utilizaremos la Distribución t en Python para realizar esta estimación.
import numpy as np
# Datos de las calificaciones de una muestra
calificaciones = [85, 90, 92, 88, 87, 84, 91, 89, 86, 87]
# Nivel de confianza (1 - alfa)
confianza = 0.95
# Grados de libertad
df = len(calificaciones) - 1
# Media y desviación estándar de la muestra
media_muestra = np.mean(calificaciones)
desviacion_muestra = np.std(calificaciones, ddof=1) # Usamos ddof=1 para calcular la desviación estándar muestral
# Valor crítico de t
valor_critico = stats.t.ppf((1 + confianza) / 2, df)
# Error estándar
error_estandar = desviacion_muestra / np.sqrt(len(calificaciones))
# Límites del intervalo de confianza
intervalo_inferior = media_muestra - valor_critico * error_estandar
intervalo_superior = media_muestra + valor_critico * error_estandar
print(f"Intervalo de confianza al {confianza * 100}%: ({intervalo_inferior:.2f}, {intervalo_superior:.2f})")
En este ejemplo, utilizamos scipy.stats.t.ppf para encontrar el valor crítico de t, calculamos el error estándar y luego estimamos el intervalo de confianza para la media de la muestra de calificaciones.
Tal y como visto, la Distribución t de Student es una herramienta esencial en estadística y análisis de datos, y su aplicación en Python facilita su uso en la práctica. Hemos visto ejemplos de cómo realizar pruebas de hipótesis y estimar intervalos de confianza utilizando la Distribución t en Python. Estas son solo algunas de las muchas aplicaciones que esta distribución ofrece en el mundo del análisis de datos.
La comprensión de la Distribución t y su implementación en Python es esencial para la toma de decisiones informadas y la realización de análisis estadísticos sólidos. ¡Hasta la próxima!