En esta publicación hablaremos sobre un concepto que puede resultar bastante confuso y que se nos presenta bastante a menudo y en distintas situaciones en la estadística: los grados de libertad.

Es muy común memorizar los grados de libertad que le corresponde a cada método (prueba t de Student, F de Fisher, χ²) sin comprender realmente lo que representan. En parte, esto puede deberse a que se trata de un concepto difícil de entender a la primera y no se suele explicar de manera extensa en la mayoría de los libros de texto.

Es por esto, que en este artículo nos hemos propuesto explicar el significado de los grados de libertad de manera simple, intuitiva, para todos y con ayuda de ejemplos prácticos. ¡Comencemos!

¿Qué son los grados de libertad?

En la estadística inferencial, el término grados de libertad se define normalmente como el número de observaciones que son libres de variar, dada una o más restricciones matemáticas, en un conjunto de valores utilizados para estimar alguna característica de la población.

Dicho de otra manera, los grados de libertad son el número de observaciones independientes menos el número de restricciones asociado a esas observaciones.

Ahora que ya tenemos la definición, veamos más de cerca los grados de libertad en el contexto del cálculo de la varianza de una muestra y la prueba t de Student.

Grados de libertad en el cálculo de la varianza muestral

Seguramente, la primera vez donde nos encontramos este concepto es a la hora de calcular la varianza de una muestra, medida que representa la variabilidad de un conjunto de datos de una muestra y que se calcula mediante la siguiente fórmula:

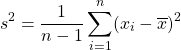
donde

• x_i es valor la observación número i.
• x̄ es la media de la muestra.
• n es el número de observaciones en la muestra.

En esta formula, los grados de libertad se encuentran en el denominador y equivalen al número de observaciones menos 1 (n – 1), por lo que solo tenemos una única restricción. 

Esta restricción se debe a que para calcular la varianza muestral es necesario calcular previamente la media de la muestra (x̄), por lo que el último valor y única observación que no es libre de variar, se puede obtener fácilmente utilizando el resto de observaciones.

Asimismo, en el caso de la media muestral, los grados de libertad equivalen al número de observaciones n, ya que no contamos con ninguna restricción.

A modo de ejemplo, imaginemos que tenemos una muestra con 5 observaciones, sabemos que la media muestral corresponde a 8 y queremos calcular la varianza muestral. La restricción que se debe cumplir consiste en que la suma de todos los datos (x₁ + x₂ + x₃ + x₄ + x₅) debe ser igual a n × x̄, en este caso, 5 × 8 = 40.

Otra manera de verlo es que la suma de las desviaciones de las observaciones con respecto a la media (x₁ – x̄, x₂ – x̄, x₃ – x̄, x₄ – x̄ y x₅ – x̄) debe ser igual a cero.

Con esta restricción, tenemos que los primeros 4 valores pueden ser cualquier número, pero para que los 5 valores sumen 40, el último valor no puede variar. Por lo tanto, tenemos 4 grados de libertad.

Así, si los primeros 4 valores son 6, 6, 8 y 10, sabemos automáticamente que el último valor corresponde a 10, ya que la suma de los 5 números debe ser igual a 40. Así de simple.

Si utilizásemos n para calcular la varianza, estaríamos subestimando la variabilidad de la población. Por ello, recurrimos a n – 1 para conseguir una estimación no sesgada de la varianza de la población.

Grados de libertad de una prueba t de Student

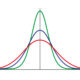
Los grados de libertad también son necesarios en la distribución t de Student ya que caracterizan la forma de la curva. Cuantos mas grados de libertad, más acampanada será la forma de la curva y por lo tanto más se asemejará a una distribución normal estándar.

En el caso de la distribución t de Student tenemos que los grados de libertad corresponden a n – 1 cuando tenemos una sola muestra y (n₁ – 1) + (n₂ – 1) si estamos comparando dos muestras.

En el primero de los casos, usamos una prueba t de Student, por ejemplo, para comprobar si la diferencia entre la media de una muestra y el valor de la hipótesis nula es estadísticamente significante.

Para ello, a hora de calcular el valor p para rechazar o no la hipótesis nula, debemos utilizar n – 1 grados de libertad al igual que en el caso anterior. Esta perdida de un grado de libertad se debe a que hemos tenido que calcular la estimación de la media previamente.

Por otro lado, si lo que queremos es utilizar la distribución t de Student para demostrar que existe diferencia entre las medias de las dos muestras, deberemos calcular el valor p usando (n₁ – 1) + (n₂ – 1) grados de libertad. Esto se debe a que hemos tenido que calcular dos medias y por lo tanto se han reducido en 2 los grados de libertad.

Espero que os haya podido solucionar vuestras dudas sobre los grados de libertad. Si aún así, no te ha quedado claro, deja tus dudas en los comentarios.

También te puede interesar: