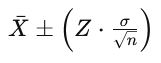En el vasto campo de la estadística, los intervalos de confianza emergen como herramientas indispensables que trascienden las simplificaciones de las estimaciones puntuales. Este artículo se adentra en la esencia de los intervalos de confianza, explorando su significado, método de cálculo y su rol crucial en proporcionar una medida más precisa y realista de la incertidumbre en el análisis estadístico.
Fundamentos de los Intervalos de Confianza
Los intervalos de confianza se erigen como regiones estadísticas que abarcan un rango probable de valores alrededor de una estimación puntual. A diferencia de las estimaciones puntuales, que proporcionan solo un valor específico, los intervalos de confianza reconocen la inherente variabilidad en las muestras y brindan una visión más completa de la posible dispersión de los valores poblacionales.
Importancia y valor de los Intervalos de Confianza
1. Superando la limitación de las estimaciones puntuales
La importancia radica en la capacidad de los intervalos de confianza para superar la limitación de las estimaciones puntuales, reconociendo la incertidumbre y ofreciendo un enfoque más robusto para interpretar datos. Proporcionan una representación visual de la variabilidad plausible en los resultados.
2. Evaluación de la precisión estadística
Los intervalos de confianza no solo ofrecen estimaciones; también incluyen un margen de error que proporciona una medida cuantificable de la precisión estadística. Un intervalo de confianza estrecho sugiere mayor precisión, mientras que uno más amplio indica mayor incertidumbre.
Cálculo y estructura de los Intervalos de Confianza
El proceso de construcción de un intervalo de confianza implica la utilización de la estimación puntual, el margen de error y el nivel de confianza deseado. La fórmula general es:
Intervalo de Confianza = Estimador Puntual ± (Margen de Error)
El margen de error se calcula considerando el error estándar y el nivel de confianza, que representa la probabilidad de que el intervalo capture el verdadero valor de la población.
Interpretación de un Intervalo de Confianza
1. Nivel de Confianza: Probabilidad de contener el parámetro
El nivel de confianza establece la probabilidad de que el intervalo de confianza capture el verdadero valor del parámetro poblacional. Un nivel de confianza del 95%, por ejemplo, sugiere que hay un 95% de probabilidad de que el intervalo contenga el valor poblacional.
2. Margen de Error: Reflejo de la precisión Estadística
El margen de error indica cuánto puede variar la estimación puntual. Un margen de error más pequeño refleja una mayor precisión en la estimación, mientras que uno más amplio sugiere mayor incertidumbre.