Los intervalos de confianza son una herramienta fundamental en la estadística inferencial, permitiéndonos estimar parámetros poblacionales a partir de datos muestrales. Sin embargo, su correcta interpretación a menudo presenta desafíos. Este artículo busca desmitificar los intervalos de confianza, proporcionando una guía clara y concisa sobre cómo entenderlos y utilizarlos adecuadamente. Exploraremos los fundamentos teóricos, los métodos de cálculo, los errores comunes y ejemplos prácticos en diversas disciplinas científicas.
Fundamentos de los Intervalos de Confianza
Un intervalo de confianza proporciona un rango de valores dentro del cual se espera que se encuentre el verdadero valor de un parámetro poblacional con un cierto nivel de confianza. Este nivel de confianza se expresa generalmente como un porcentaje (por ejemplo, 95%, 99%).
Formalmente, un intervalo de confianza se define como:
[Límite Inferior, Límite Superior]
Donde:
- Límite Inferior (LI) es el valor mínimo del rango.
- Límite Superior (LS) es el valor máximo del rango.
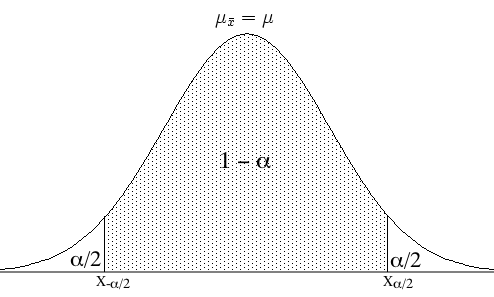
El nivel de confianza (1 – α) representa la probabilidad de que el intervalo contenga el verdadero parámetro, donde α es el nivel de significancia.
Por ejemplo, un intervalo de confianza del 95% implica que, si repitiéramos el muestreo y el cálculo del intervalo muchas veces, el 95% de los intervalos resultantes contendrían el verdadero valor del parámetro. Es crucial entender que no significa que haya un 95% de probabilidad de que el verdadero valor esté dentro de un intervalo específico ya calculado.
Factores que Afectan el Intervalo de Confianza:
- Tamaño de la Muestra (n): A mayor tamaño de la muestra, menor será la amplitud del intervalo de confianza, ya que la estimación será más precisa.
- Nivel de Confianza (1 – α): A mayor nivel de confianza, mayor será la amplitud del intervalo.
- Desviación Estándar (σ): Una mayor variabilidad en los datos (mayor desviación estándar) resultará en intervalos más amplios.
Ejemplo:
Supongamos que queremos estimar la altura promedio de los estudiantes de una universidad. Tomamos una muestra de 100 estudiantes y encontramos que la altura promedio es de 170 cm, con una desviación estándar de 5 cm. Para calcular un intervalo de confianza del 95%, podemos usar la siguiente fórmula (asumiendo una distribución normal):
Intervalo de Confianza = Media ± (Z * (Desviación Estándar / √(Tamaño de la Muestra)))Donde Z es el valor crítico de la distribución normal estándar correspondiente al nivel de confianza deseado. Para un nivel de confianza del 95%, Z ≈ 1.96.
Por lo tanto:
Intervalo de Confianza = 170 ± (1.96 * (5 / √100)) = 170 ± 0.98El intervalo de confianza del 95% para la altura promedio de los estudiantes es [169.02 cm, 170.98 cm].
Cálculo e Interpretación Correcta
El cálculo de un intervalo de confianza depende del tipo de parámetro que se esté estimando (media, proporción, diferencia de medias, etc.) y de la distribución de los datos. Aquí presentamos algunos ejemplos comunes:
1. Intervalo de Confianza para la Media (población normal, σ conocida):
Si la población se distribuye normalmente y la desviación estándar de la población (σ) es conocida, el intervalo de confianza para la media (μ) se calcula como:
Intervalo de Confianza = x̄ ± (Z * (σ / √n))Donde:
- x̄ es la media muestral.
- Z es el valor crítico de la distribución normal estándar.
- σ es la desviación estándar de la población.
- n es el tamaño de la muestra.
2. Intervalo de Confianza para la Media (población normal, σ desconocida):
Si la desviación estándar de la población es desconocida, se utiliza la distribución t de Student:
Intervalo de Confianza = x̄ ± (t * (s / √n))Donde:
- t es el valor crítico de la distribución t de Student con (n-1) grados de libertad.
- s es la desviación estándar muestral.
3. Intervalo de Confianza para una Proporción:
Para estimar la proporción (p) de una población, se utiliza la siguiente fórmula:
Intervalo de Confianza = p̂ ± (Z * √((p̂ * (1 - p̂)) / n))Donde:
- p̂ es la proporción muestral.
Interpretación Correcta:
- Un intervalo de confianza no indica la probabilidad de que el verdadero parámetro esté dentro del intervalo calculado.
- La interpretación correcta es que, si se repitiera el muestreo muchas veces, el (1 – α)% de los intervalos calculados contendrían el verdadero valor del parámetro.
- El nivel de confianza refleja la confiabilidad del proceso de estimación, no la certeza de que el parámetro esté en un intervalo específico.
Es importante tener en cuenta que los intervalos de confianza se basan en supuestos sobre la distribución de los datos. Si estos supuestos no se cumplen, el intervalo puede ser inexacto.
Errores Comunes al Usar Intervalos de Confianza
El uso incorrecto de los intervalos de confianza puede llevar a conclusiones erróneas. Algunos errores comunes incluyen:
1. Interpretar el Nivel de Confianza como Probabilidad:
Como se mencionó anteriormente, un intervalo de confianza del 95% no significa que haya un 95% de probabilidad de que el verdadero parámetro esté dentro del intervalo. Significa que, si repitiéramos el muestreo muchas veces, el 95% de los intervalos calculados contendrían el verdadero valor.
2. Confundir Significación Estadística con Significación Práctica:
Un intervalo de confianza estrecho puede indicar significación estadística, pero no necesariamente significación práctica. Es decir, el efecto estimado puede ser estadísticamente significativo pero demasiado pequeño para ser relevante en el mundo real.
3. Ignorar los Supuestos del Modelo:
Los intervalos de confianza se basan en ciertos supuestos, como la normalidad de los datos o la independencia de las observaciones. Si estos supuestos no se cumplen, el intervalo puede ser inexacto. Es crucial verificar los supuestos antes de interpretar un intervalo de confianza.
4. Usar Intervalos de Confianza para Hacer Declaraciones Definitivas:
Los intervalos de confianza proporcionan un rango de valores plausibles para el parámetro, no una única respuesta definitiva. Es importante reconocer la incertidumbre inherente en la estimación estadística y evitar hacer afirmaciones categóricas basadas únicamente en el intervalo de confianza.
5. No Considerar el Tamaño del Efecto:
Un intervalo de confianza puede ser estadísticamente significativo, pero el tamaño del efecto puede ser pequeño. Siempre es importante considerar la magnitud del efecto además de la significancia estadística.
Ejemplo de Código (Python):
import numpy as np
import scipy.stats as st
data = np.array([15, 18, 20, 22, 25, 17, 21, 19, 24, 23])
# Cálculo del intervalo de confianza del 95% usando la distribución t
confidence_interval = st.t.interval(0.95, len(data)-1, loc=np.mean(data), scale=st.sem(data))
print("Intervalo de confianza del 95%:", confidence_interval)Ejemplos en Diferentes Áreas Científicas
Los intervalos de confianza se utilizan en una amplia variedad de disciplinas científicas para estimar parámetros y tomar decisiones informadas.
1. Medicina:
Ensayos clínicos utilizan intervalos de confianza para estimar la eficacia de un tratamiento. Por ejemplo, un intervalo de confianza para la diferencia en la tasa de curación entre un nuevo fármaco y un placebo puede indicar si el fármaco es significativamente mejor que el placebo.
2. Economía:
Los economistas utilizan intervalos de confianza para estimar parámetros como el crecimiento del PIB, la tasa de inflación y la tasa de desempleo. Estos intervalos proporcionan una medida de la incertidumbre asociada con las estimaciones y ayudan a los responsables de la formulación de políticas a tomar decisiones informadas.
3. Psicología:
En la investigación psicológica, los intervalos de confianza se utilizan para estimar la magnitud de un efecto, como la diferencia en el rendimiento entre dos grupos o la correlación entre dos variables. Por ejemplo, un intervalo de confianza para la diferencia en las puntuaciones de ansiedad entre un grupo de tratamiento y un grupo de control puede indicar si el tratamiento es eficaz.
4. Ingeniería:
Los ingenieros utilizan intervalos de confianza para estimar la fiabilidad de un componente o sistema. Por ejemplo, un intervalo de confianza para el tiempo medio hasta el fallo de un dispositivo puede ayudar a los ingenieros a diseñar productos más fiables.
5. Ciencias Ambientales:
Los científicos ambientales utilizan intervalos de confianza para estimar parámetros como la concentración de contaminantes en el agua o el aire. Estos intervalos ayudan a evaluar el impacto de las actividades humanas en el medio ambiente.
Ejemplo:
En un estudio sobre la efectividad de un nuevo fertilizante en el rendimiento de los cultivos de maíz, se encontró que el rendimiento promedio con el nuevo fertilizante fue de 120 bushels por acre, con un intervalo de confianza del 95% de [115, 125]. Esto sugiere que, con un 95% de confianza, el verdadero rendimiento promedio con el nuevo fertilizante está entre 115 y 125 bushels por acre.
Los intervalos de confianza son una herramienta valiosa para la inferencia estadística, pero su interpretación correcta es esencial. Comprender los fundamentos teóricos, los métodos de cálculo y los errores comunes al usar intervalos de confianza permite tomar decisiones informadas y evitar conclusiones erróneas. Al considerar los intervalos de confianza en el contexto de la investigación científica, es crucial tener en cuenta el tamaño de la muestra, el nivel de confianza, los supuestos del modelo y la significación práctica de los resultados.