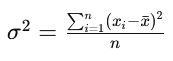Entendiendo la Varianza: Claves para Interpretar la Dispersión de Datos
La varianza es una medida fundamental en estadística que nos proporciona información crucial sobre la dispersión de datos dentro de un conjunto. Comprender este concepto es esencial para cualquier análisis significativo. En este artículo, exploraremos la varianza, su significado y cómo interpretarla para obtener una visión más completa de nuestros datos.
¿Qué es la Varianza y por qué es importante?
La varianza es una medida estadística que cuantifica la dispersión de un conjunto de datos. En otras palabras, nos dice qué tan dispersos o agrupados están los valores en torno a la media. Una varianza baja indica que los datos tienden a estar cerca de la media, mientras que una varianza alta sugiere una mayor dispersión.
Fórmula de la Varianza: Un vistazo rápido
La fórmula para calcular la varianza (σ²) es la siguiente:
Donde:
- n es el número de observaciones en el conjunto de datos.
- xi representa cada valor individual en el conjunto de datos.
- x̄ es la media del conjunto de datos.
Interpretando la Varianza: Claves para el análisis
Varianza Baja: Datos agrupados
Una varianza baja indica que los valores en el conjunto de datos están cerca de la media. Esto sugiere una mayor homogeneidad y menor dispersión. Es común encontrar una baja varianza en conjuntos de datos donde los valores son relativamente similares entre sí.
Varianza Alta: Datos dispersos
Por el contrario, una varianza alta señala que los valores están más dispersos alrededor de la media. Este escenario sugiere una mayor heterogeneidad y una mayor variabilidad entre los datos. Conjuntos de datos con una varianza alta pueden mostrar una amplia gama de valores.
Varianza y Desviación Estándar: Una relación importante
La desviación estándar (σ) es simplemente la raíz cuadrada de la varianza. Ambas medidas proporcionan información similar sobre la dispersión de los datos, pero la desviación estándar tiene la ventaja de estar en la misma escala que los datos originales.
Utilidad de la Varianza en la toma de decisiones
Evaluación de riesgos
En finanzas y ciencias actuales, entender la varianza es crucial. Se utiliza para evaluar el riesgo asociado con inversiones y pronosticar la volatilidad en los mercados.
Control de calidad
En la producción y manufactura, la varianza se utiliza para monitorear la consistencia y calidad de los productos. Una baja varianza indica una producción más consistente.
Limitaciones y Consideraciones
Aunque la varianza es una herramienta valiosa, no es inmune a las peculiaridades de los datos. Puede verse afectada por valores extremos, y en algunos casos, la interpretación pura de la varianza puede ser limitada.
Entender la varianza es esencial para cualquier analista de datos. Sirve como una brújula que guía nuestra interpretación de la dispersión de datos. Ya sea en finanzas, ciencias o control de calidad, la varianza es una herramienta poderosa para evaluar la homogeneidad de los datos y tomar decisiones informadas basadas en la variabilidad de los resultados. ¡Incorpora la varianza en tu caja de herramientas estadísticas y descubre un nuevo nivel de comprensión en tus análisis de datos!