Distribución t de Student: Funcionamiento, propiedades y aplicaciones en estadística
La estadística es una disciplina esencial en el análisis de datos, y entre sus herramientas más valiosas se encuentra la Distribución t de Student. En este artículo, exploraremos en profundidad qué es la Distribución t de Student, cómo funciona, sus propiedades clave y sus diversas aplicaciones en estadística. Desde pruebas de hipótesis hasta la estimación de intervalos de confianza, la Distribución t desempeña un papel fundamental en la toma de decisiones basadas en datos.
¿Qué es la Distribución t de Student y por qué es importante?
La Distribución t de Student, a menudo conocida simplemente como la Distribución t, es una distribución de probabilidad que se emplea para modelar datos que siguen una distribución normal y que tienen tamaños de muestra pequeños. Su nombre proviene del seudónimo «Student,» utilizado por el estadístico británico William Sealy Gosset, quien desarrolló esta distribución a principios del siglo XX mientras trabajaba en la cervecería Guinness.
La importancia de la Distribución t radica en su capacidad para abordar muestras pequeñas, donde la varianza poblacional es desconocida. En tales casos, la Distribución t proporciona una herramienta valiosa para realizar inferencias estadísticas con mayor precisión que la Distribución normal estándar (Z).
Historia de la Distribución t de Student
Como ya hemos comentado, la historia de la Distribución t se remonta a principios del siglo XX. William Sealy Gosset, un joven estadístico empleado en la cervecería Guinness en Irlanda, se encontró con el desafío de desarrollar métodos estadísticos para controlar la calidad de la cerveza. Dado que las muestras de cerveza eran pequeñas y la varianza poblacional era desconocida, Gosset se aventuró a encontrar una solución.
En 1908, Gosset publicó un artículo en el que introdujo la Distribución t como una solución para la estimación de la media de muestras pequeñas. Su trabajo revolucionó la estadística y allanó el camino para la creación de pruebas de hipótesis y estimación de intervalos de confianza basados en la Distribución t.
Propiedades de la Distribución t de Student
La Distribución t tiene varias propiedades clave que la hacen valiosa en estadística:
- Simetría: La Distribución t es simétrica alrededor de su media, al igual que la Distribución normal.
- Colas Pesadas: Una de las características distintivas de la Distribución t es que tiene colas más pesadas en comparación con la Distribución normal. Esto significa que es menos sensible a valores atípicos y extremos.
- Parámetro de Grados de Libertad: El parámetro crítico que influye en la forma de la Distribución t es el número de grados de libertad (df). Cuanto mayor sea el número de grados de libertad, más se asemejará la Distribución t a una Distribución normal. De esto ya hablamos previamente en este artículo.
Funcionamiento de la Distribución t de Student
El funcionamiento de la Distribución t se basa en la relación entre la media de una muestra y la media poblacional, ajustada por el tamaño de la muestra y la varianza poblacional desconocida. La fórmula general para la Distribución t es la siguiente:
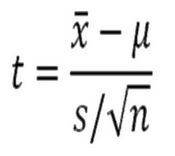
Donde:
- t es el valor de la Distribución t.
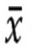es la media de la muestra.- μ es la media poblacional (generalmente desconocida).
- es la desviación estándar de la muestra.
- n es el tamaño de la muestra.
El valor t calculado se compara con los valores críticos de la Distribución t para determinar la significancia estadística de una prueba de hipótesis o la construcción de un intervalo de confianza.
Funcionamiento de la Distribución t de Student
La Distribución t se utiliza en diversas aplicaciones en estadística y análisis de datos:
- Pruebas de Hipótesis: La Distribución t se utiliza para realizar pruebas de hipótesis sobre la media de una población cuando el tamaño de la muestra es pequeño y la varianza poblacional es desconocida. Permite determinar si las diferencias observadas son estadísticamente significativas.
- Intervalos de Confianza: Se emplea para estimar intervalos de confianza para la media de una población, lo que proporciona una medida de incertidumbre en la estimación.
- Regresión Lineal: En análisis de regresión, la Distribución t se aplica para realizar pruebas de significancia sobre los coeficientes de regresión, lo que ayuda a determinar si las variables independientes son significativas.
- Comparación de Medias: Se utiliza para comparar las medias de dos grupos y determinar si existen diferencias significativas entre ellos. Por ejemplo, se emplea en pruebas t pareadas para comparar los resultados antes y después de una intervención.
El número de grados de libertad (df) es un parámetro clave que influye en la forma de la Distribución t. Cuanto mayor sea el número de grados de libertad, más se asemejará la Distribución t a una Distribución normal. En la Distribución t estándar, con infinitos grados de libertad, la Distribución t se convierte en la Distribución normal estándar (Z).
En la práctica, utilizamos tablas o software estadístico para buscar valores críticos de t basados en el número de grados de libertad y el nivel de confianza deseado. Esto nos permite realizar pruebas de hipótesis y construir intervalos de confianza de manera precisa.
Ejemplos de Aplicación de la Distribución t de Student
- Estimación de Intervalos de Confianza: Supongamos que tenemos una muestra de 30 mediciones de la altura de árboles. Utilizamos la Distribución t para estimar un intervalo de confianza del 95% para la altura promedio de todos los árboles en el bosque.
- Prueba de Hipótesis: Imagina que una empresa lanza un nuevo producto y quiere saber si la satisfacción del cliente es mayor que cierto valor de referencia. Utilizamos la Distribución t para realizar una prueba de hipótesis y tomar una decisión basada en los datos recopilados.
- Comparación de Medias: Una organización quiere determinar si dos métodos de capacitación producen diferencias significativas en el desempeño de los empleados. La Distribución t se emplea para comparar las medias de los dos grupos de empleados y determinar si existen diferencias significativas.
Como hemos visto en este artículo, la Distribución t de Student es una herramienta esencial en estadística y análisis de datos, especialmente cuando trabajamos con muestras pequeñas y desconocemos la varianza de la población. Desde pruebas de hipótesis hasta la estimación de intervalos de confianza, la Distribución t juega un papel fundamental en la toma de decisiones basadas en datos.
En futuros artículos, mostraremos como se utiliza con Python mediante diversos ejemplo y exploraremos aplicaciones más avanzadas de la Distribución t. Si tienes alguna pregunta, no dudes en comentar. ¡Hasta la próxima!
